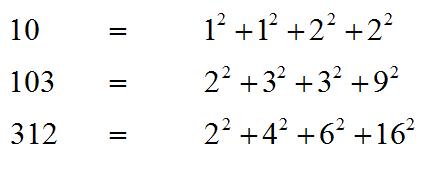Casa
four square theorem

Euler Four-Square Identity -- from Wolfram MathWorld

Por um escritor misterioso

Descrição
The amazing polynomial identity communicated by Euler in a letter to Goldbach on April 12, 1749 (incorrectly given as April 15, 1705--before Euler was born--in Conway and Guy 1996, p. 232). The identity also follows from the fact that the norm of the product of two quaternions is the product of the norms (Conway and Guy 1996).
Euler Four-Square Identity -- from Wolfram MathWorld
Lagrange's Four-Square Theorem -- from Wolfram MathWorld
Euler Four-Square Identity -- from Wolfram MathWorld
Euler Formula -- from Wolfram MathWorld
Euler Four-Square Identity -- from Wolfram MathWorld
Euler's four-square identity - Wikipedia
Euler Four-Square Identity -- from Wolfram MathWorld
Pi - Wikiversity
Euler Four-Square Identity -- from Wolfram MathWorld
Memory SpringerLink
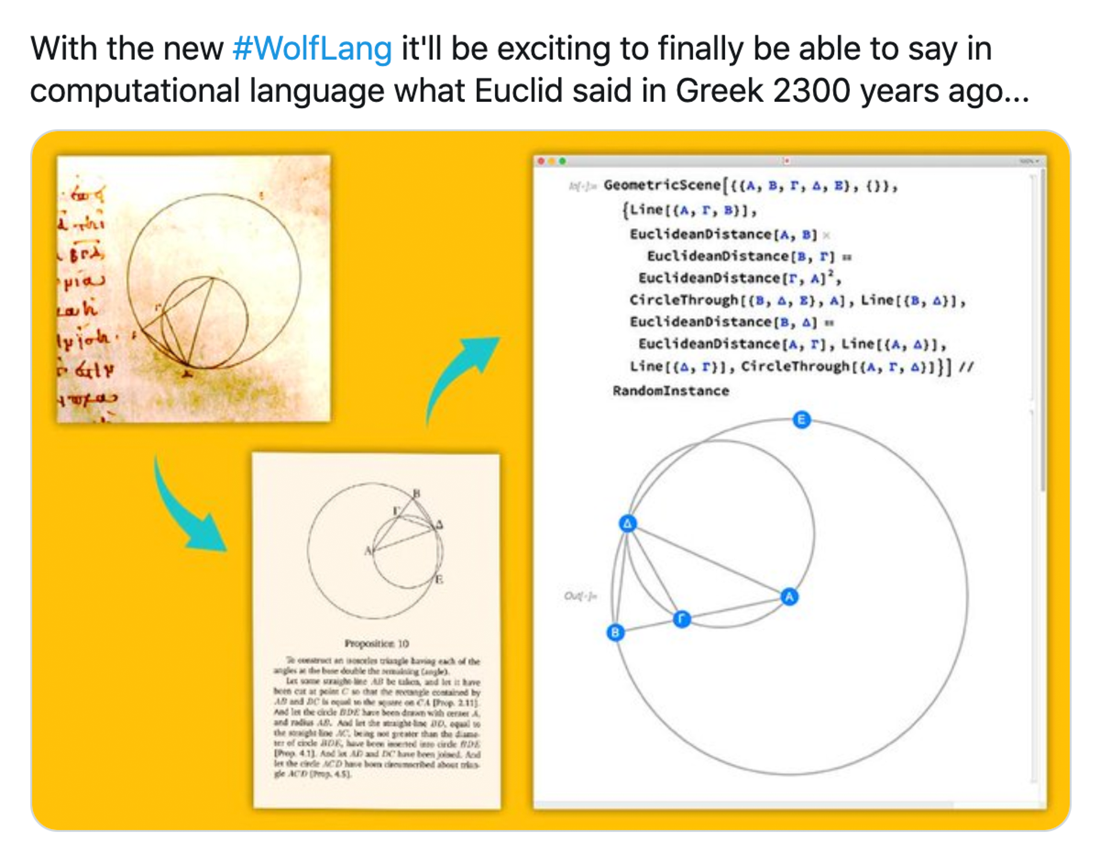
Euler Four-Square Identity -- from Wolfram MathWorld
The Empirical Metamathematics of Euclid and Beyond—Stephen Wolfram
Euler Four-Square Identity -- from Wolfram MathWorld
Square (algebra) - Wikipedia
Euler Four-Square Identity -- from Wolfram MathWorld
Complex Numbers – Mathematical Mysteries
Euler Four-Square Identity -- from Wolfram MathWorld
Reply to @bus_.driver an example of an Euler brick and the
Euler Four-Square Identity -- from Wolfram MathWorld
Polynomial Identity -- from Wolfram MathWorld
Euler Four-Square Identity -- from Wolfram MathWorld
Open problem in number theory
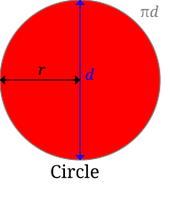
Euler Four-Square Identity -- from Wolfram MathWorld
Pi, Number in Math Wiki
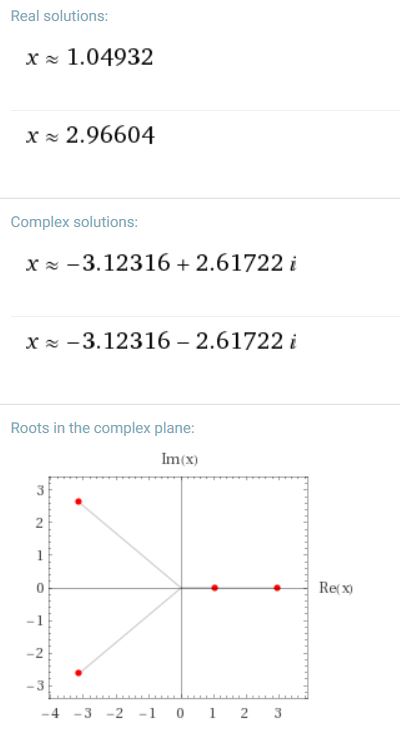
Euler Four-Square Identity -- from Wolfram MathWorld
mathematics Archives - The Billy Lee Pontificator
Euler Four-Square Identity -- from Wolfram MathWorld
The Universe of Discourse: category 'math/se
Euler Four-Square Identity -- from Wolfram MathWorld
What is the value of n, if 1 - 1/2 + 1/3 - 1/4 + … - 1/2012 + 1
de por adulto (o preço varia de acordo com o tamanho do grupo)