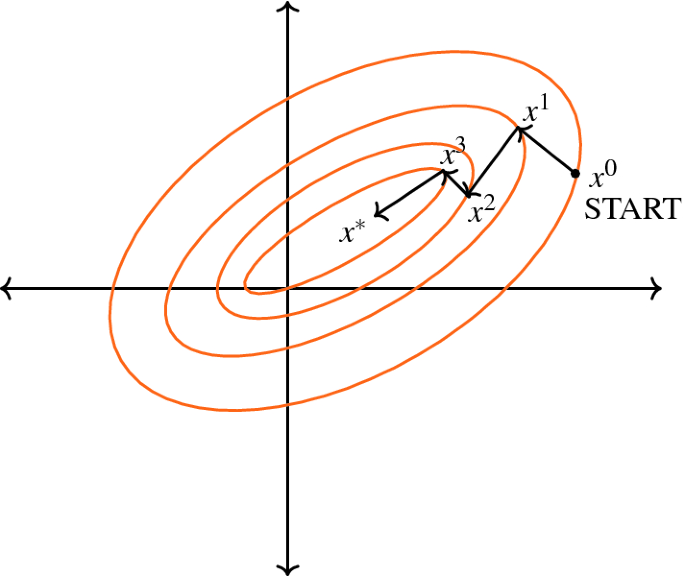
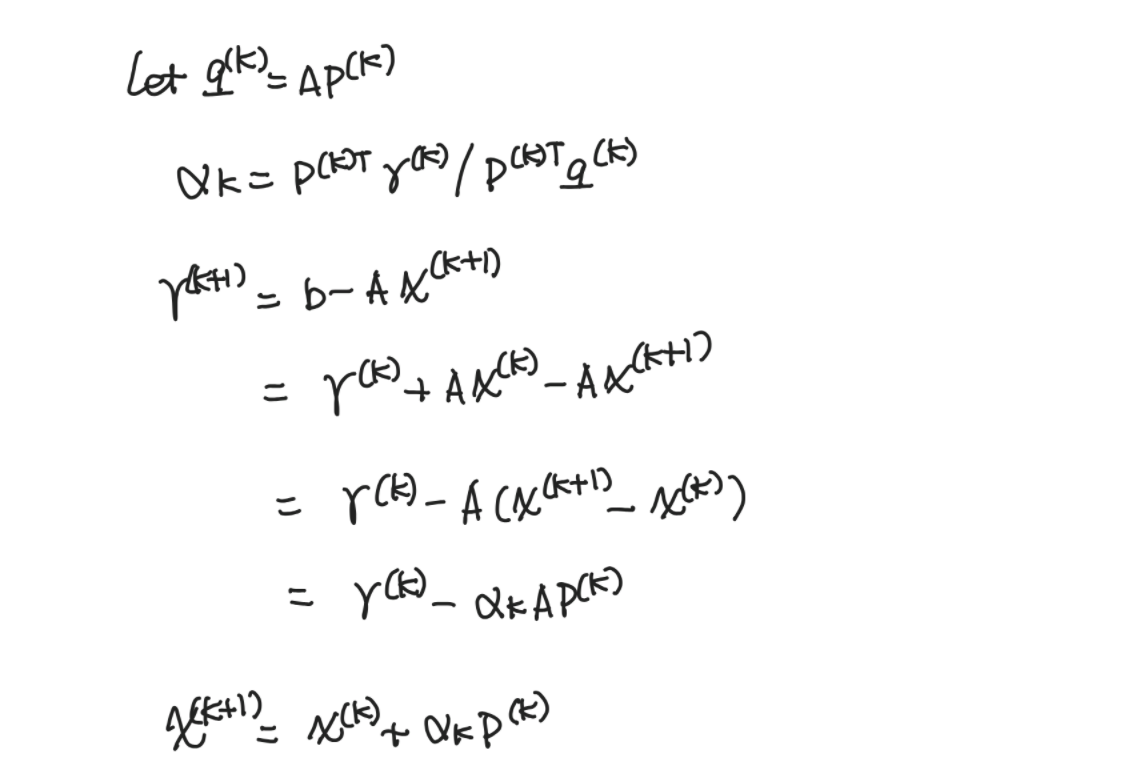MathType - The #Gradient descent is an iterative optimization #algorithm for finding local minimums of multivariate functions. At each step, the algorithm moves in the inverse direction of the gradient, consequently reducing
Por um escritor misterioso
Descrição
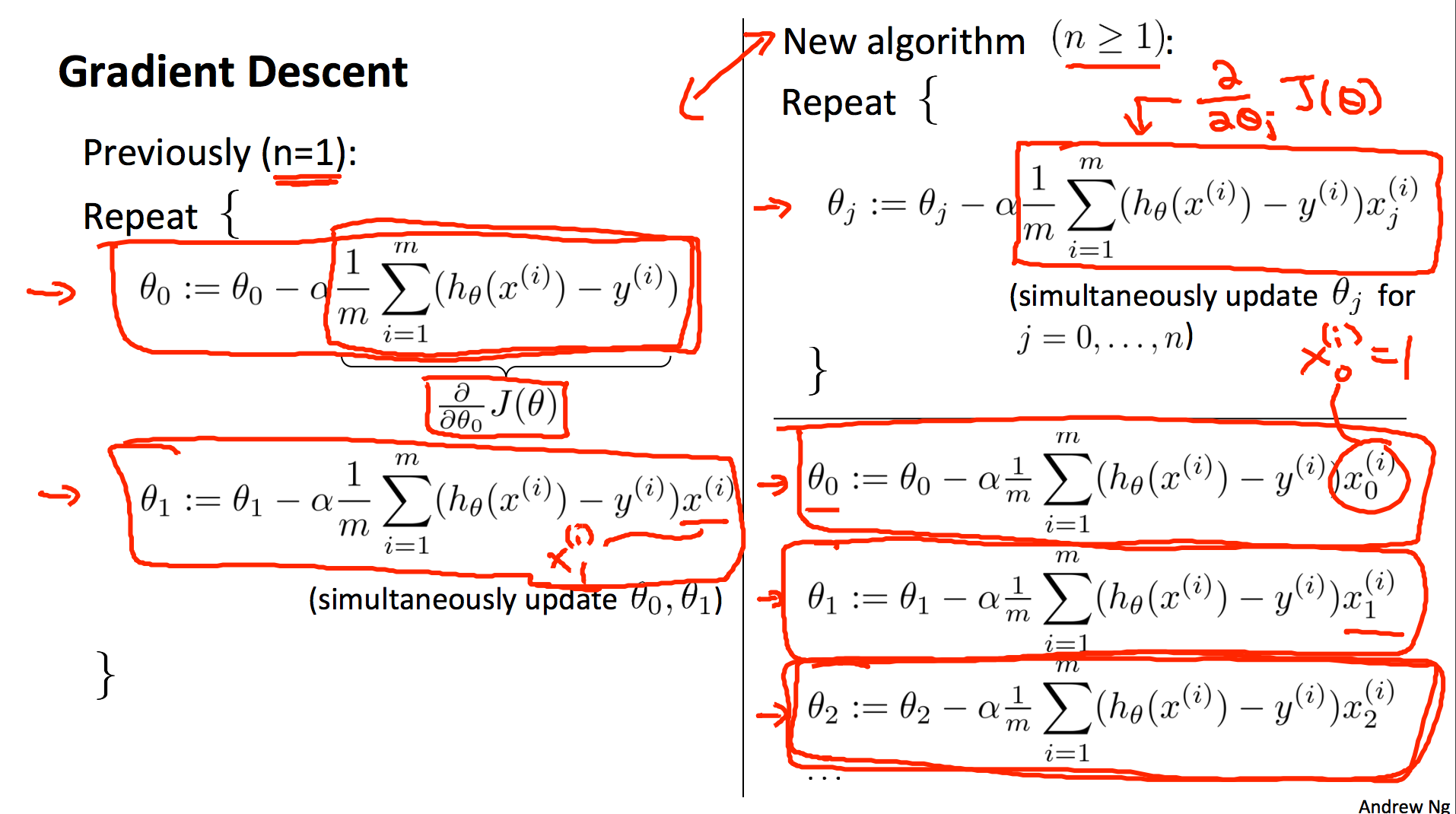
L2] Linear Regression (Multivariate). Cost Function. Hypothesis. Gradient
In mathematical optimization, why would someone use gradient descent for a convex function? Why wouldn't they just find the derivative of this function, and look for the minimum in the traditional way?

Solved Gradient descent is a first-order iterative
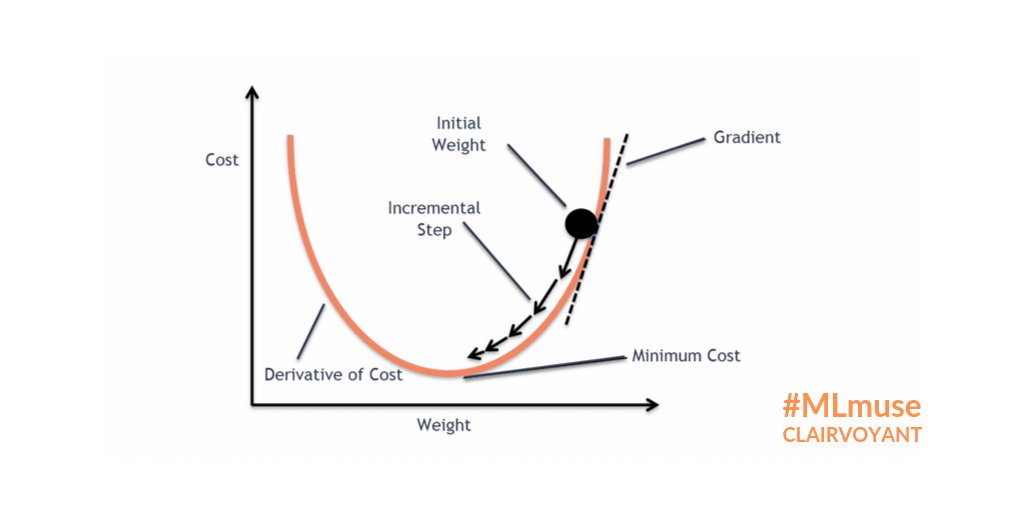
Gradient descent algorithm and its three types
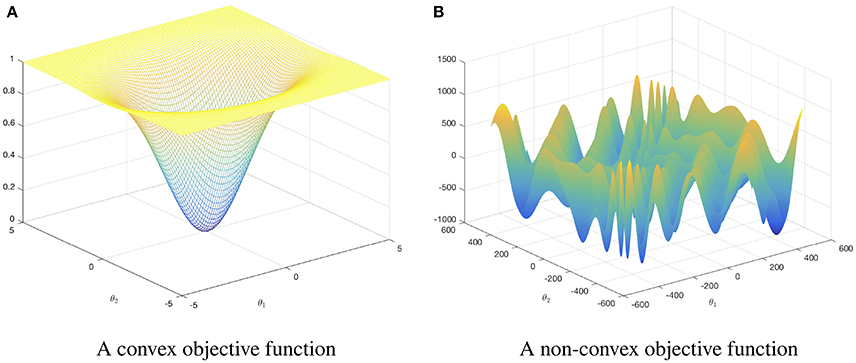
Gradient Descent Algorithm
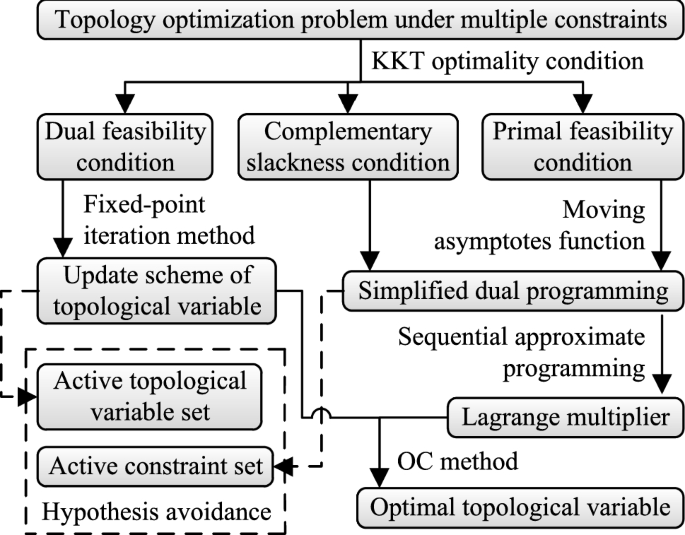
An optimality criteria method hybridized with dual programming for topology optimization under multiple constraints by moving asymptotes approximation
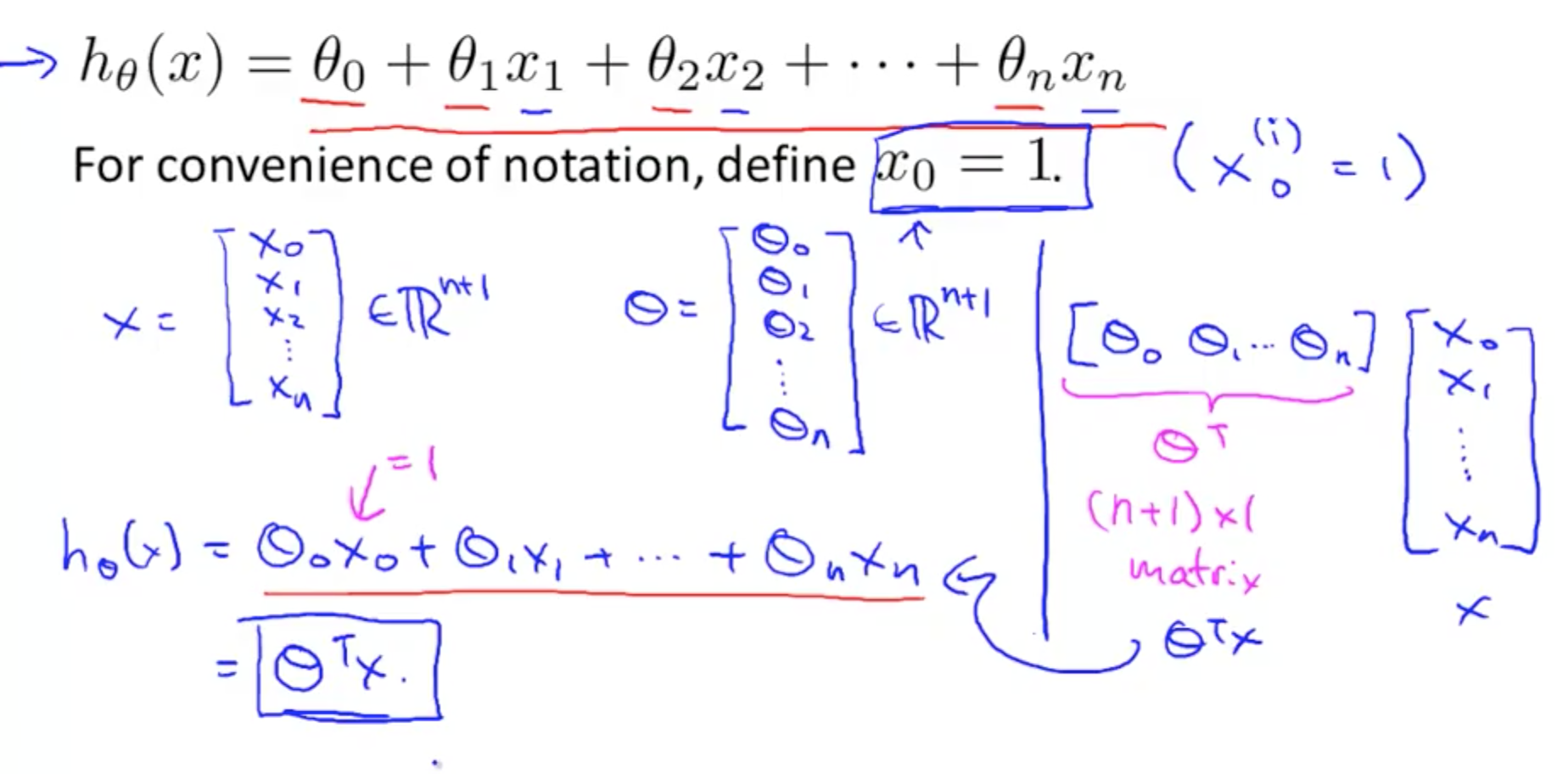
Linear Regression with Multiple Variables Machine Learning, Deep Learning, and Computer Vision

Conditional gradient method for multiobjective optimization

Solved Problem 4 (a) Compute one iteration of the gradient
de
por adulto (o preço varia de acordo com o tamanho do grupo)